

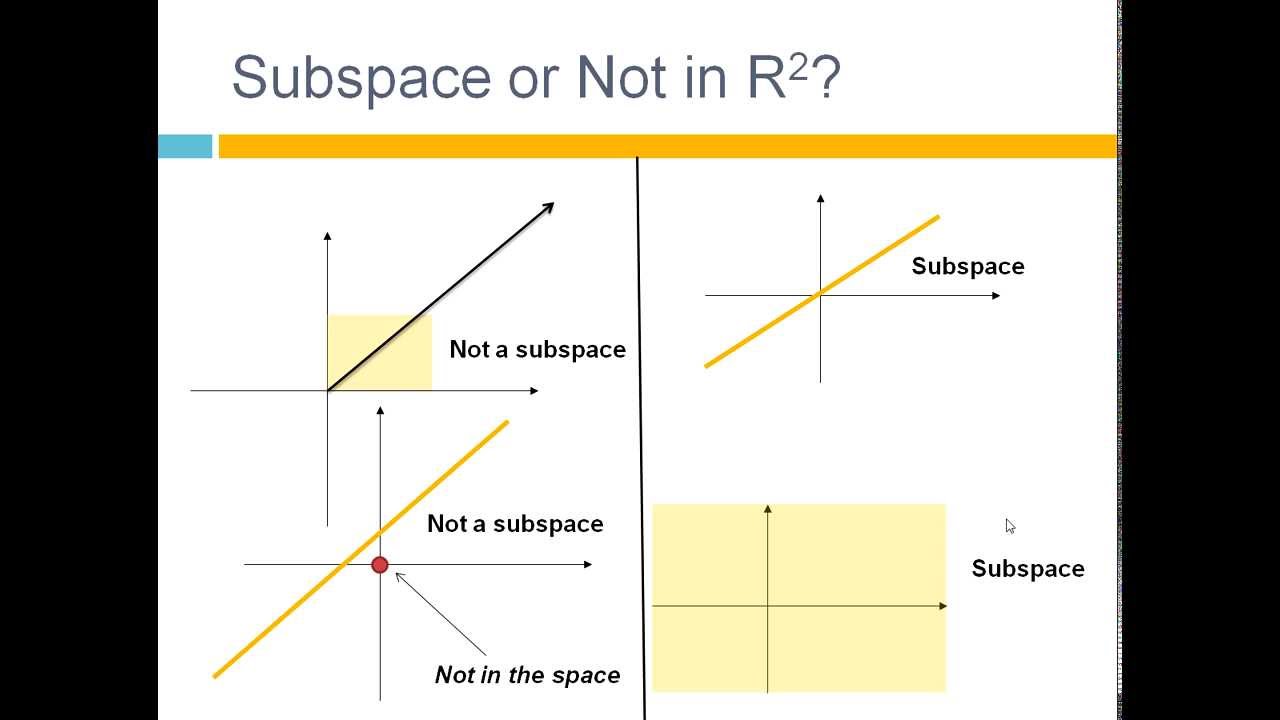
It gets easier and easier to believe the more the exercise is done. It is possible to mathematically prove this but it does not add much intuition - instead, think of the mental image of adding (tail-to-head) and stretching our two vectors, and seeing that the result still ends up on the plane. By substituting constants a and b we can create any vector in the plane. The technical word for this is the span of the linear combination. You can imagine two vectors in 3d space going in different directions, and having a plane that goes through both of them. Let’s first see two vectors that don’t define the entirety of R² space.Īny combination of the blue vector and the red vector will result in a vector that lies on the green plane. We can define R² by taking a linear combination of any two vectors that are not on the same line. Everything else we will be describing after this are vector subspaces - basically, seeing if we can find smaller spaces that are contained within our larger vector spaces like R².įor example, if our failed “1st quadrant subspace” was actually a proper subspace that was closed under multiplication and addition, it would be a subspace of R², since it dealt with finding spaces within the vector space (therefore, subspaces) of R². Therefore, our R² system is closed under multiplication and addition, and although it may seem a little obvious, is technically a space. There is no way you can add any 2D vectors or multiply them by a scalar and leave the dimension of R², like somehow going from a = to a =. Say we define our space to be all 2 dimensional vectors where x and y are both positive.Įvery vector on the 2D cartesian plane is within the subspace of R².

To better understand this, let’s take a case where we don’t satisfy this criteria for a proper vector space. If we can take a linear combination for all vectors v and w in a subspace and all real-numbered scalars c or v and still stay inside some space S, we have a valid vector space. Together, we can combine the operations of vector addition and scalar multiplication to get a linear combination, which is in the format c v + d w. If we have a ‘vector space’ S and we have vectors v and w, which both belong to the group S, v + w (vector addition) must also belong in S and so does c v or d w (multiplication where c and d are scalars). What is a Vector Space?Ī vector space, and later, subspaces, are a group of vectors that are closed under scalar multiplication and addition.

We can analyze the rows and columns of our matrix A to understand the concept of vector spaces and subspaces. Now that we have fundamentally covered the elimination way of looking at a system of equations Ax = b, we can delve a little more into the abstract concepts of linear algebra that underlie the system.
#SUBSPACE DEFINITION LINEAR ALGEBRA SERIES#
If Gaussian Elimination seems foreign, I have a series of three articles walking through the meanings and mechanics of it. This article assumes knowledge of Gaussian Elimination, matrix multiplication, linear combinations, and a few other concepts. Sub spacesĪ nonempty subset of vector space for which closure holds for addition and scalar multiplication is called a subspace.Delving into real linear algebra with column space and vector spaces Now, checking (checking for all the elements would not possible because of enormous number of elements in set) if closure holds for addition for set N.Ĭlosure holds for multiplication for set N. Closure LawĪ set is said to be closure under an operation (like addition, subtraction, multiplication, etc.) if that operation is performed on elements of that set and result also lies in set.įor example, N is a set of all natural numbers. If the vectors, A = are linearly independent then the basis of vector space would be same as span.īefore we go into vector sub spaces, we will look at Closure law from Discrete Mathematics. Yes, because vector space also the set of all linear combinations of all the vectors inside it just like a span. The number of elements in set of Basis is equal to Dimension of vector space. If one more vector from vector space is added to the Basis set, the set will become linearly dependent. Basisīiggest set of linearly independent vectors in a vector space is called Basis. So, if we assume a vector space V, then the dimension of that vector space ( dim V) will be maximum number of linearly independent vectors in V. Maximum number of linearly independent vectors in a vector space is called Dimension of that vector space. So to generalize this, Vector space Rⁿ consist of all the n-tuple vectors and their linear combinations where each element of tuple is a real number. R³ vector space, it contains all the vectors (that have 3 elements each) and their linear combinations


 0 kommentar(er)
0 kommentar(er)
